上一篇文章我们简单介绍了一下什么是图,以及用JS来实现一个可以添加顶点和边的图。按照惯例,任何数据结构都不可或缺的一个point就是遍历。也就是获取到数据结构中的所有元素。那么图当然也不例外。这篇文章我们就来看看如何遍历以及用js来实现图的遍历。
首先,有两种算法可以对图进行遍历:广度优先搜索(BFS)和深度优先搜索(DFS)。图的遍历可以用来寻找特定的顶点,可以寻找两个顶点之间有哪些路径,检查图是否是联通的,也可以检查图是否含有环等等。
在开始代码之前,我们需要了解一下图遍历的思想,也就是说,我们要知道如何去遍历一个图,知道了图遍历的方法方式,距离实现代码也就不远了。
图遍历的思想是:
1、必须追踪每个第一次访问的节点,并且追踪有哪些节点还没有被完全探索。对于BFS和DFS两种算法,都需要明确给出第一个被访问的顶点。
2、完全探索一个顶点,要求我们查看该顶点的每一条边。对于每一条边所链接的没有被访问过的顶点,将其标注为被发现的,并将其加入到待访问顶点列表中。
那么,总结一下上面的两句话,首先,我们在遍历一个图的时候,需要指定第一个被访问的顶点是什么(也就是我们要在方法中传入第一个顶点的值)。然后呢.....我们需要知道三个状态:
一个是还未被访问的,也就是我还不知道有这么个顶点,也不知道它的边都去向哪里。
另外一个是已经访问过但未被探索过,就是说,我知道有这个顶点,但是我不知道它的边都去向哪里,连接着哪些顶点。
最后一个是访问过并且完全探索过。也就是我访问过该顶点,也探索过它有哪些边,它的边连接哪些顶点。
那么,我们就会在构造函数中用三种颜色来代表上面的三种状态,分别是白色(未被访问),灰色(已经访问过但未被探索过)和黑色(访问过并且完全探索过);
还有另外一个要注意的地方,BFS和DFS在算法上其实基本上是一样的,但是有一个明显的不同——待访问顶点的数据结构。BFS用队列来存储待访问顶点的列表,DFS用栈来存储待访问顶点的列表。
好了,下面我们来上代码。(这里不会贴上所有的代码,只会贴上有关BFS和DFS的相关代码。)
如果你看到了这里,但是并不觉得自己可以耐心的把下面的代码看完,那么你看到这里就可以 结束所有有关于用js来实现数据结构的内容了。如果你还是想继续往下学习,那么希望你一定可以耐心看完整。
//引入前面章节学过的栈和队列,因为我们后面会用到。function Stack () {};function Queue() {};function Graph() { var vertices = []; var adjList = new Map(); //添加顶点的方法。 this.addVertices = function (v) {}; this.addEdge = function (v,w) {}; this.toString = function () {}; //初始化图中各顶点的状态(颜色)的私有方法,并返回该状态数组。 var initializeColor = function () { var color = []; for (var i = 0; i < vertices.length; i++) { color[vertices[i]] = 'white'; } return color; }; //简单的广度优先搜索算法,传入参数v是图中的某一个顶点,从此顶点开始探索整个图。 this.bfs = function (v,callback) { //为color状态数组赋值,初始化一个队列 var color = initializeColor(),queue = new Queue(); //将我们传入的顶点v入队。 queue.enqueue(v); // 如果队列非空,也就是说队列中始终有已发现但是未探索的顶点,那么执行逻辑。 while(!queue.isEmpty()) { // 队列遵循先进先出的原则,所以我们声明一个变量来暂时保存队列中的第一个顶点元素。 var u = queue.dequeue(); // adjList是我们的邻接表,从邻接表中拿到所有u的邻接顶点。 neighbors = adjList.get(u); //并把状态数组中的u的状态设置未已发现但是未完全探索的灰色状态。 color[u] = 'grey'; //我们循环当前的u的所有的邻接顶点,并循环访问每一个邻接顶点并改变它的状态为灰色。 for(var i = 0; i < neighbors.length; i++) { var w = neighbors[i]; if (color[w] === "white") { color[w] = 'grey'; //入队每一个w,这样while循环会在队列中没有任何元素,也就是完全访问所有顶点的时候结束。 queue.enqueue(w); } } // 完全访问后设置color状态。 color[u] = 'black'; // 如果存在回调函数,那么就执行回掉函数。 if(callback) { callback(u); } } }; //改进后计算最短路径的BFS // 其实这里改进后的BFS并没有什么特别复杂,只是在原有的bfs的基础上,增加了一些需要计算和储存的状态值。 // 也就是我们在函数结束后所返回的 this.BFS = function (v) { //d是你传入的顶点v距离每一个顶点的距离(这里的距离仅为边的数量) //pred就是当前顶点沿着路径找到的前一个顶点是什么。没有就是null var color = initializeColor(),queue = new Queue(),d = [],pred = []; //我们把v入队。 queue.enqueue(v); //初始化距离和前置点数组。一个都为0,一个都为null,无需解释。 for(var i = 0; i < vertices.length; i++) { d[vertices[i]] = 0; pred[vertices[i]] = null; } while(!queue.isEmpty()) { var u = queue.dequeue(); neighbors = adjList.get(u); color[u] = 'grey'; for(var i = 0; i < neighbors.length; i++) { var w = neighbors[i]; if (color[w] === "white") { color[w] = 'grey'; // 到这里都和bfs方法是一样的,只是多了下面这两个。 // 这里容易让人迷惑的是w和u分别是啥?弄清楚了其实也就没啥了。 // u是队列中出列的一个顶点,也就是通过u来对照邻接表找到所有的w。 // 那么因为是d(距离,初始为0)。所以我们只要在d的数组中w的值设为比u大1也就是d[u] + 1就可以了 d[w] = d[u] + 1; // 而这个就不用说了,理解了上面的,这个自然就很好懂了。 pred[w] = u; // 这里可能大家会问,循环不会重复加入么?不会! // 注意看这里if (color[w] === "white")这句,如果是white状态才会执行后面的逻辑, // 而进入逻辑后,状态就随之改变了,不会再次访问到访问过的顶点。 queue.enqueue(w); } } color[u] = 'black'; } return { distances:d, predecessors:pred } }; //深度优先搜索 // 这个没啥东西大家自己看一下就可以了 this.dfs = function (callback) { var color = initializeColor(); for(var i = 0; i < vertices.length; i++) { if(color[vertices[i]] === 'white') { // 这里调用我们的私有方法 dfsVisit(vertices[i],color,callback); } } }; //深度优先搜索私有方法 // 从dfs中传入的三个参数 var dfsVisit = function (u,color,callback) { // 改变u的颜色状态 color[u] = 'grey'; if(callback) {callback(u);} // 获取所有u的邻接顶点 var neighbors = adjList.get(u); // 循环 for(var i = 0; i < neighbors.length; i++) { //w为u的每一个邻接顶点的变量 var w = neighbors[i]; // 如果是白色的我们就递归调用dfsVisit if(color[w] === 'white') { dfsVisit(w,color,callback); } } color[u] = 'black'; }; //改进后的DFS,其实也就是加入了更多的概念和要记录的值 this.DFS = function () { // d,发现一个顶点所用的时间。f,完全探索一个顶点所用的时间,p前溯点。 var color = initializeColor(),d = [],f = [], p = []; // 初始化时间为0; time = 0; //初始化所有需要记录的对象的值/ for(var i = 0; i < vertices.length; i++) { f[vertices[i]] = 0; d[vertices[i]] = 0; p[vertices[i]] = null; } for (var i = 0; i < vertices.length; i++) { if(color[vertices[i]] === 'white') { DFSVisit(vertices[i],color,d,f,p); } } return { discovery:d, finished:f, predecessors:p } }; //注意这里我们为什么要在外层定义时间变量,而不是作为参数传递进DFSVisit。 //因为作为参数传递在每次递归的时候time无法保持一个稳定变化的记录。 var time = 0; //这里个人觉得也没什么好说的了,如果你看不懂,希望你可以数据结构系列的第一篇看起。 var DFSVisit = function (u,color,d,f,p) { console.log('discovered--' + u); color[u] = 'grey'; d[u] = ++time; var neighbors = adjList.get(u); for (var i = 0; i < neighbors.length; i++) { var w = neighbors[i]; if (color[w] === 'white') { p[w] = u; DFSVisit(w,color,d,f,p); } } color[u] = 'black'; f[u] = ++time; console.log('explored--' + u); };} 上面是有关于BFS和DFS的代码及注释。希望大家可以认真耐心的看完。下面我们来看看简单的最短路径算法和拓扑排序。
1、最短路径算法
//最短路径,也就是说我们在地图上,想要找到两个点之间的最短距离(我们经常会用地图软件来搜索此地与彼地的路径)。//那么下面我们就以连接两个顶点之间的边的数量的多少,来计算一下各自的路径,从而得到一个最短路径。// 我们通过改进后的BFS算法,可以得到下面这样的数据,各个顶点距离初始顶点的距离以及前溯点var shortestPathA = graph.BFS(verticesArray[0]);console.log(shortestPathA)/*distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F:2,G:2,H:2,I:3],predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F:"B",G:"C",H:"D",I:"E"]*///我们选择数组中的第一个元素为开始的顶点。var fromVertex = verticesArray[0];for(var i = 1; i < verticesArray.length;i++) { // 到达的定点不定 var toVertex = verticesArray[i]; //声明路径为一个初始化的栈。 path = new Stack(); //嘿嘿,这个循环比较有趣了,通常大家都会用var i= 0; i < xxx;i++这种。 //但是这里这么用是几个意思?首先大家要知道for循环中两个“;”所分割的三个语句都是什么意思。 //语句 1 在循环(代码块)开始前执行,语句 2 定义运行循环(代码块)的条件,语句 3 在循环(代码块)已被执行之后执行 //所以我们怎么写都是可以的!!当然你要符合你想要的逻辑 //后面就不说了,没啥好说的。 for(var v = toVertex;v!== fromVertex;v = shortestPathA.predecessors[v]) { path.push(v); } path.push(fromVertex); var s = path.pop(); while(!path.isEmpty()) { s += '-' + path.pop(); } console.log(s)}/*A-BA-CA-DA-B-EA-B-FA-C-GA-D-HA-B-E-I*/ 2、拓扑排序
,想了想,还是有必要给大家解释一下概念再开始代码,不然真的容易一脸懵逼。
大家先来看张图:
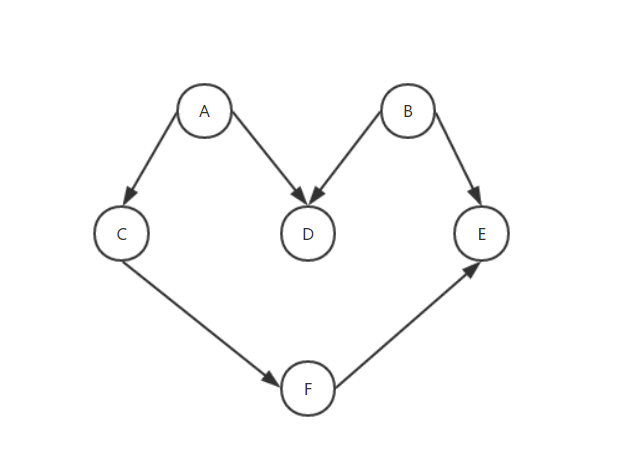
那,这是一个什么东西呢?这是一个有向图,因为边是有方向的,这个图没有环,意味着这是一个无环图。所以这个图可以称之为有向无环图。那么有向无环图可以做什么呢?我记得前面某一篇文章说过,所有的实例都有其所面对的要解决的实际问题。而有向无环图可以视作某一个序列的待执行的任务,该任务不是可跳跃的。比如一个产品上线,需要产品经理定需求,画流程图,再到UI出效果图标注图再到开发再到测试再到改bug再到上线。就是这个意思。
那么我们上面所形容的产品上线的整个流程就成为拓扑排序。拓扑排序只能应用于DAG(有向无环图)。
那么我们看下代码。
//重新声明一个图并所有的顶点加入图中。var DFSGraph = new Graph();var DFSarray = ["a","b","c","d","e","f"];for (var i = 0; i < DFSarray.length; i++) { DFSGraph.addVertices(DFSarray[i]);}//我们为图加上边。DFSGraph.addEdge("a","c");DFSGraph.addEdge("a","d");DFSGraph.addEdge("b","d");DFSGraph.addEdge("b","e");DFSGraph.addEdge("c","f");DFSGraph.addEdge("f","e");var result = DFSGraph.DFS();console.log(result);//大家自己去看看打印的结果是什么。 那么到这里,有关于图的一部分内容基本上就都讲解完毕了。可能大家觉得我有些偷懒,注释写的没有以前那么详细了啊。这是因为我觉得很多的内容前面都已经很详细的说明过了。同样的思路实在是没必要翻来覆去的说来说去。所以反而到后面一些复杂的数据结构并没有前面解释的那么详细。但是我觉得如果你一路看下来,这点东西绝壁难不倒你。
最后,由于本人水平有限,能力与大神仍相差甚远,若有错误或不明之处,还望大家不吝赐教指正。非常感谢!